Heap Sort
Overview:
žUses a heap as its data structure
žIn-place sorting algorithm – memory efficient
žTime complexity – O(n log(n))
What is a Heap?
A heap is also known as a priority queue and can be represented by a binary tree with the following properties:
Structure property: A heap is a completely filled binary tree with the exception of the bottom row, which is filled from left to right.
Heap Order property:For every node x in the heap, the parent of x greater than or equal to the value of x.
(known as a max-heap).
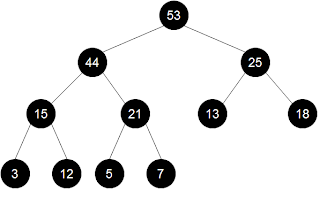
Example: a heap
Algorithm
Step
1. Build Heap – O(n)
- Build binary tree taking N items as input, ensuring the heap structure property is held, in other words,
build a complete binary tree.
- Build binary tree taking N items as input, ensuring the heap structure property is held, in other words,
build a complete binary tree.
- Heapify the
binary tree making sure the binary tree satisfies the Heap Order property.
Step
2. Perform n deleteMax operations – O(log(n))
- Delete the maximum element in the heap –
which is the root node, and place this element at the end of
the sorted array.
the sorted array.
Simplifying things
For speed and efficiency we can represent the heap with an array. Place the root at array index 1, its left child at index 2, its right child at index 3, so on and so forth…
For
any node i, the following formulas apply:
The
index of its parent = i / 2
Index
of left child = 2 * i
Index
of right child = 2 * i + 1
Sample Run
žStart
with unordered array of data
Array
representation:
21 15 25 3 5 12 7 19 45 2 9
Binary tree representation:
21 15 25 3 5 12 7 19 45 2 9
Binary tree representation:
Tags
MCA




Checkout other sorting programs here.....
ReplyDeleteHeap Sort in C
Bubble Sort in C
Insertion Sort in C
Selection Sort in C
Quick Sort in C